Four inverted pieces puzzle

Solving an nameless puzzle with paper, scissors and eventually code. In collaboration with Sarah Perrone.
Published on May 20, 2023 by Francesca Priante
Recreational mathematics Puzzles
Few weeks ago my collegue and friend Sarah came to the office and told me “Do you want to try to solve a puzzle? It has no name, I found it in a small shop in my hometown, the cashier saw it in a science museum in Paris and replicated it from memory using wood.”
The premise was intriguing: “let’s try” I said.
She didn’t have the original piece because she gave it to a friend, so she took paper and scissor and made it out.
The game goes like this: there are 4 red pieces and 4 blue pieces in a row, with a empty space in the middle of the 2 groups (as in the image - we only had red and pink paper).
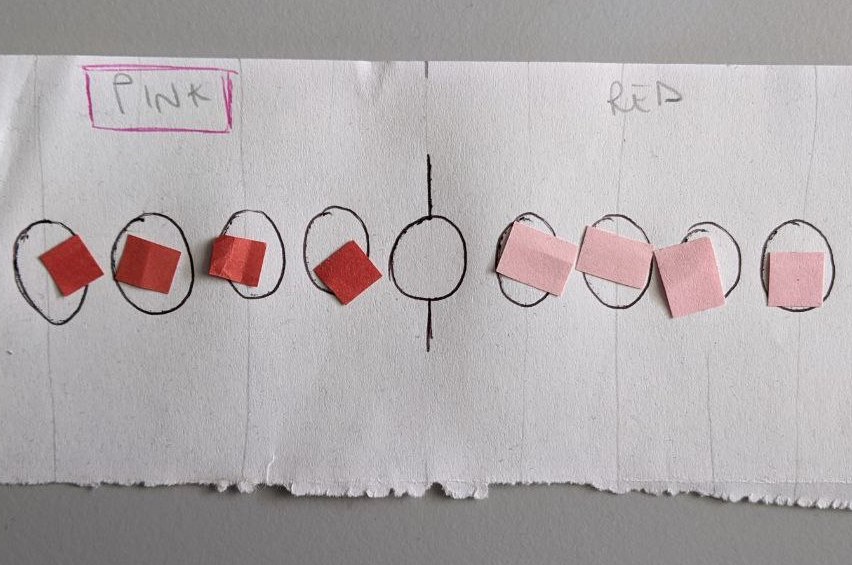 Crafting the game with paper
Crafting the game with paper
At the beginning of the game all the 4 red pieces are on the left, and all the blue pieces on the right. The aim of the game is to move all the red to the right and all the blue to the left. The rules are pretty simple:
- A piece can be moved where the empty space is if it is right next to it (shift)
- A piece can also be moved where the empty space is if between the two there is a piece of the opposite color (jump). I.e. a red piece can jump over a single blue piece, and vice versa.
Analysis section
Well, we spent the whole lunch break trying to solve it, but without any success.
So we said “Let’s try to break it down to simpler steps”. We tried the simplest possible case: 2 pieces, 1 red and 1 blue (here I’m using A and B letters for semplicity):
| step | configuration | agent | move type |
|---|---|---|---|
| 1 | A_B | ||
| 2 | _AB | A | shift |
| 3 | BA_ | B | jump |
| 4 | B_A | A | shift |
Ok this was too easy, let’s try with 2 pieces per color.
| step | configuration | agent | move type |
|---|---|---|---|
| 1 | AA_BB | ||
| 2 | A_ABB | A | shift |
| 3 | ABA_B | B | jump |
| 4 | ABAB_ | B | shift |
| 5 | AB_BA | A | jump |
| 6 | _BABA | A | jump |
| 7 | B_ABA | B | shift |
| 8 | BBA_A | B | jump |
| 9 | BB_AA | A | shift |
Ok it gets interesting, here we started noticing something:
- The number of steps needed are squared numbers. In particular they seem to follow the square of the number of pieces of one color added by 1. Given \(n\) number of pieces:
subtract 1 to the squared value because the number of steps are one less the the total number of configurations
- List of moves are symmetric. In the \(n=2\) example we see that at the 5-th step the agent and the move types are mirrored. It makes sense since the two group of pieces have to exchange in positions and mirror the initial configuration.
Let’s see if it generalizes, if it does it means that with n=3 we would have 16 configurations and 15 move to solve it.
| step | configuration | agent | move type |
|---|---|---|---|
| 1 | AAA_BBB | ||
| 2 | AA_ABBB | A | shift |
| 3 | AABA_BB | B | jump |
| 4 | AABAB_B | B | shift |
| 5 | AAB_BAB | A | jump |
| 6 | A_BABAB | A | jump |
| 7 | _ABABAB | A | shift |
| 8 | BA_ABAB | B | jump |
| 9 | BABA_AB | B | jump |
| 10 | BABABA_ | B | jump |
| 11 | BABAB_A | A | shift |
| 12 | BAB_BAA | A | jump |
| 13 | B_BABAA | A | jump |
| 14 | BB_ABAA | B | shift |
| 15 | BBBA_AA | B | jump |
| 16 | BBB_AAA | A | shift |
It does generalize!
Other patterns also emerge in the moves:
- the agents alternate themselves with increasing number of moves: 1 for A, 2 for B, 3 for A. Until the middle section where the mirroring starts. Also each block always ends with a shift and the starting moves are always jumps (exception for first and middle block)
- The number of jumps is \(n^2\)
- The number of shifts is \(2*n\)
Using this raw algorithm we finally got to solve the original 4 pieces puzzle.
Right after we wanted to know more about this game and we searched for keywords like “casse tête pions 4 museum paris”. We finally ended up in this arcticle which explains that the inventor is the mathematician Édouard Lucas. He also published an issue about this puzzle in 1883. Édouard Lucas was particularly into recreational mathematics, he is mostly known as the inventor of the Tower of Hanoi problem.
Coding section
I took inspiration from that arcticle to code the solving algorithm in python, but I made it longer but (hopefully) more self-explainatory.
In the following code block I build 2 lists: direction (-1 or 1) and action (jump or shift). A always move to the right and B always to the left so the agent specification is already encoded in the direction list.
The idea is to make a for loop for each block of steps by agent type. Example:
1st block: A shifts to the right
action = [‘shift’]
direction = [+1]
2nd block: B jumps and then shift to the left
action = [‘jump’,’shift’]
direction = [-1,-1]
import numpy as np
n = 3 # number of pieces of 1 color
# %% Prepare instructions
direction = () # -1 or 1
action = () # Jump or shift
for group in range(1, n+1):
action = np.append(action, np.append(['jump']*(group-1),'shift')) # repeat the jump group-1 times and add a shift at the end
if (group % 2) != 0:
# if group is odd
direction = np.append(direction, [1]*group)
else:
# if group is even
direction = np.append(direction, [-1]*group)
# The moves are symmetric, I add up the reversed vector at the end.
# But before, I add the center block of moves
direction_reversed = np.flip(direction)
action_reversed = np.flip(action)
# I have to move n times the other piece, different from the last move
last_move = direction[len(direction)-1]
direction = np.append(direction, [last_move*(-1)]*n)
direction = np.append(direction, direction_reversed)
# central block always jumps
action = np.append(action, ['jump']*n)
action = np.append(action, action_reversed)
check the reulting list:
np.stack((direction, action)).transpose()
array([['1.0', 'shift'],
['-1.0', 'jump'],
['-1.0', 'shift'],
['1.0', 'jump'],
['1.0', 'jump'],
['1.0', 'shift'],
['-1.0', 'jump'],
['-1.0', 'jump'],
['-1.0', 'jump'],
['1.0', 'shift'],
['1.0', 'jump'],
['1.0', 'jump'],
['-1.0', 'shift'],
['-1.0', 'jump'],
['1.0', 'shift']], dtype='<U32')
Now show in a “human readable” way the solving steps:
action_num = action
action_num[action_num=='shift']=1
action_num[action_num=='jump']=2
action_num = action_num.astype(int)
game = np.empty(( (n+1)**2, n*2+1), dtype=str)
game[0,:] = [*n * "A" + "_" + n * "B"]
space = n # The empty space is in the middle (n-th position in zero based indexing)
for i in range(len(direction)):
displacement = int(action_num[i]*direction[i])
game[i+1] = game[i]
game[i+1][space] = game[i][space - displacement] # replace the piece with the empty space
game[i+1][space - displacement] = game[i][space] # replace the empty space with the piece
space = space - displacement
print("".join(game[i+1]))
which gives:
AA_ABBB
AABA_BB
AABAB_B
AAB_BAB
A_BABAB
_ABABAB
BA_ABAB
BABA_AB
BABABA_
BABAB_A
BAB_BAA
B_BABAA
BB_ABAA
BBBA_AA
BBB_AAA
Acknowledgement
Thanks to Sarah Perrone for raising such an exciting puzzle during an extremely ordinary day.