Boids algorithm with Python

How to create beautiful flock patterns with Python!

Published on September 17, 2022 by Francesca Priante

Python

Have you ever wondered how do flocks of birds create amazing floating patterns in the sky? You may think they follow very complicated laws and unpredictable movements, but they actually follow 3 simple rules. The complexity of the flock of birds arises from the interaction of birds responding to simple rules. This type of behavior is called emergent behavior and it’s a key feature of self-organized systems.

Emergence is complexity arising from simplicity
- Kurzgesagt -

The simple rules that model pretty well this behaviour were formalized by Craig Reynolds in 1986 and state like this:

  1. Cohesion or flock centering: bird attempts to stay close to nearby flockmates.
  2. Separation or collision avoidance: bird avoids collision with nearby flockmates.
  3. Alignment or velocity matching: bird attempts to match velocity with nearby flockmates.

The 3 rules make up the boids-algorithm, and it does not apply only to birds but also to fish schools. “Boids” term comes from the union of birds-oid, which refers to all the birds-like elements.

Let’s dive into the algorithm.

Needed libraries

import numpy as np
from matplotlib import pyplot as plt
from matplotlib.animation import FuncAnimation
import random
import os
import numpy as np
from scipy.spatial.distance import pdist, squareform
import math

Set up parameters

# %% 
# Initialize plot
L = 450
fig = plt.figure()
ax = plt.axes(xlim=(-L, L), ylim=(-L, L))
points, = ax.plot([], [], '.', color = 'black')
plt.axis('off')


tsteps         = 200        # Time steps
n              = 300        # Number of birds
V0             = 20         # Initial velocity

wall_repulsion = 20         # https://vanhunteradams.com/Pico/Animal_Movement/Boids-algorithm.html#Screen-edges
margin         = 20
max_speed      = 20
neighbors_dist = 70         # Community distance (At which distance they apply rule 1 and rule 3)

# Rule 1: COHESION
R = 0.1                     # velocity to center contribution

# Rule 2: SEPARATION
bird_repulsion = 7          # low values  make more "stains" of birds, nice visualization
privacy        = 14         #  Avoid each other ,length. When they see each other at this distance, 

# Rule 3: ALIGNMENT
match_velocity = 3

Initialize boids

Give boids random position and random velocities (up to V0) at time 0.

x = np.zeros((n,tsteps))
y = np.zeros((n,tsteps))

# Randomize initial positions
x[:,0] = np.random.uniform(low=-L, high=L, size=(int(n),))
y[:,0] = np.random.uniform(low=-L, high=L, size=(int(n),))

# Randomize initial velocity
x[:,1] = x[:,0] + np.random.uniform(low=-V0, high=V0, size=(int(n),))
y[:,1] = y[:,0] + np.random.uniform(low=-V0, high=V0, size=(int(n),))

Three flock rules

Rule 1. Cohesion

First thing to do is to measure the distance between each pair of boids and check wheter the distance is lower or equal to the neighbots_dist that we set at the beginning. Then, for each boid i we compute the mean position of its neighbors (relative center of mass). We then define the velocity contribution of this step as the vector between the starting position and the relative center of mass, weighted by the coefficient R.

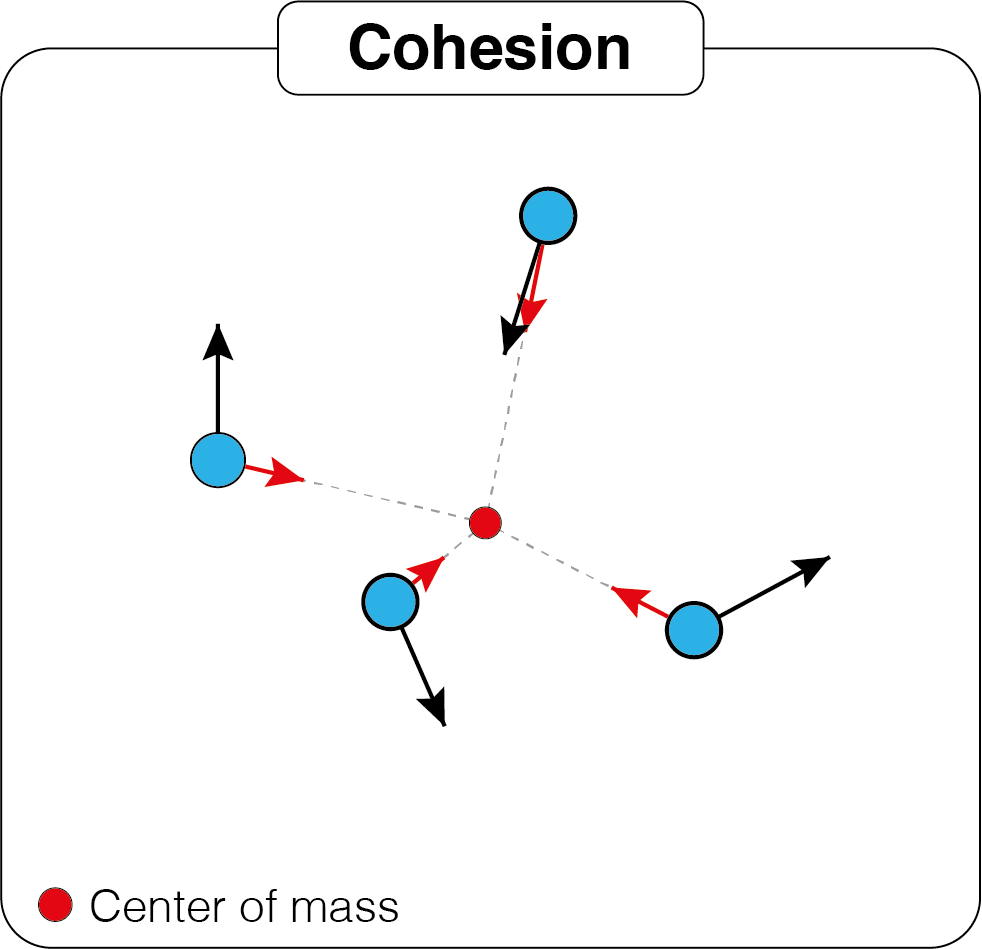
cohesion

Note: when computing the distance between each boids, I considered also the self distance of each boid, just for simplicity. So when considering the relative center of mass, the boid i position is also taken into account. But it’s negligible. You can avoid this by just uncommenting the & (m!=0).

def moveToCenter(x0, y0, neighbors_dist, n, R):
    m = squareform(pdist(np.transpose([x0,y0])))
    idx = (m<=neighbors_dist) # & (m!=0)
    
    center_x = np.zeros(n)
    center_y = np.zeros(n)
    vx = np.zeros(n)
    vy = np.zeros(n)
    for i in range(0, n-1):
        center_x[i] = np.mean(x0[idx[i,]])
        center_y[i] = np.mean(y0[idx[i,]])
        vx[i] = -(x0[i] - center_x[i])*R
        vy[i] = -(y0[i] - center_y[i])*R

    return vx,vy

Rule 2. Separation

Here the pairwise distance between pairs of boids is required to be lower than the privacy parameter to apply the bird_repulsion. The velocity contribution in this step is the distance between the 2 neighbors boids weighted by bird_repulsion and the direction is repulsive for the two boids.

idx is a 2 by m matrix, where m is the number of boids that has at least 1 neighbor invading its privacy. The 2 columns refers to the indexes of the boids that are close to each others.

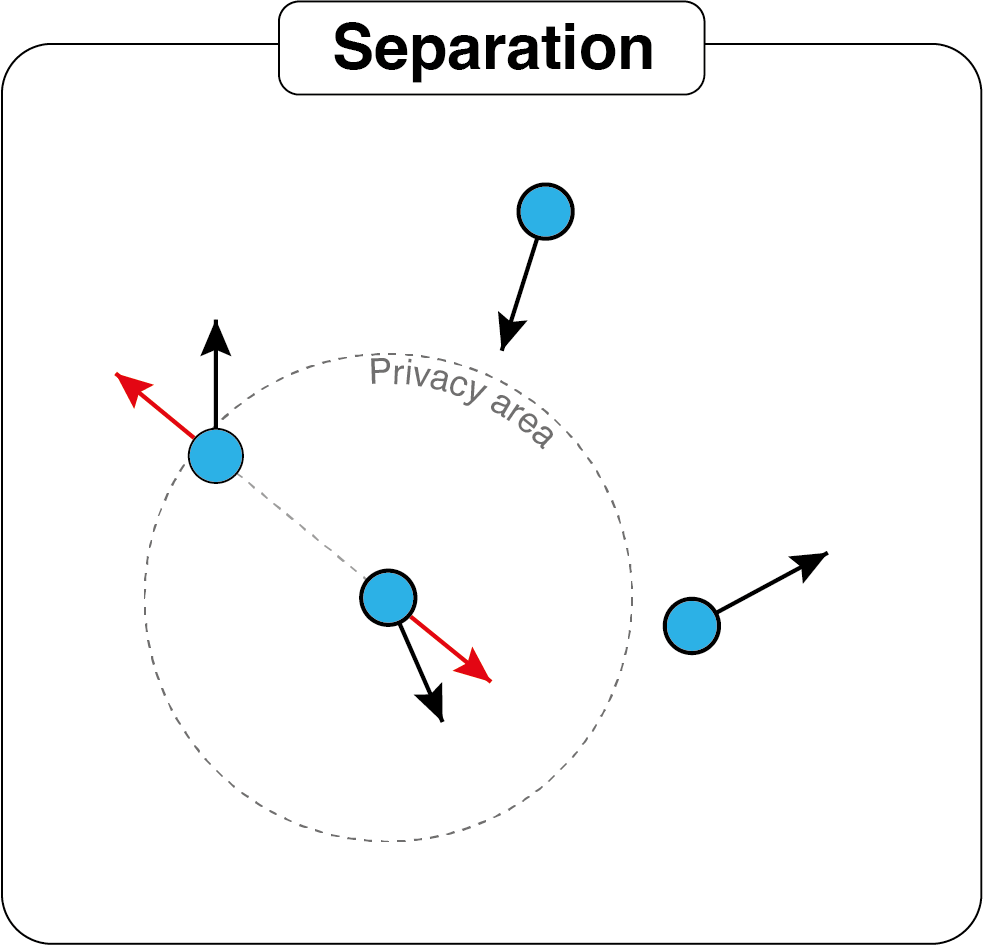
separation

def avoidOthers(x0, y0, n, privacy, bird_repulsion):
    dist = squareform(pdist(np.transpose([x0,y0])))
    
    idxmat = (dist<privacy) & (dist !=0)
    idx = np.transpose(np.array(np.where(idxmat)))
    
    vx = np.zeros(n)
    vy = np.zeros(n)
    
    vx[idx[:,0]] = (x0[idx[:,0]] - x0[idx[:,1]])*bird_repulsion
    vy[idx[:,0]] = (y0[idx[:,0]] - y0[idx[:,1]])*bird_repulsion    
    return vx,vy

Rule 3. Alignment

This rule is like the first rule, but for the velocities instead of the positions. For each boid, we compute the mean velocities of its neighbors, and we return it weighted bu match_velocity coefficient.

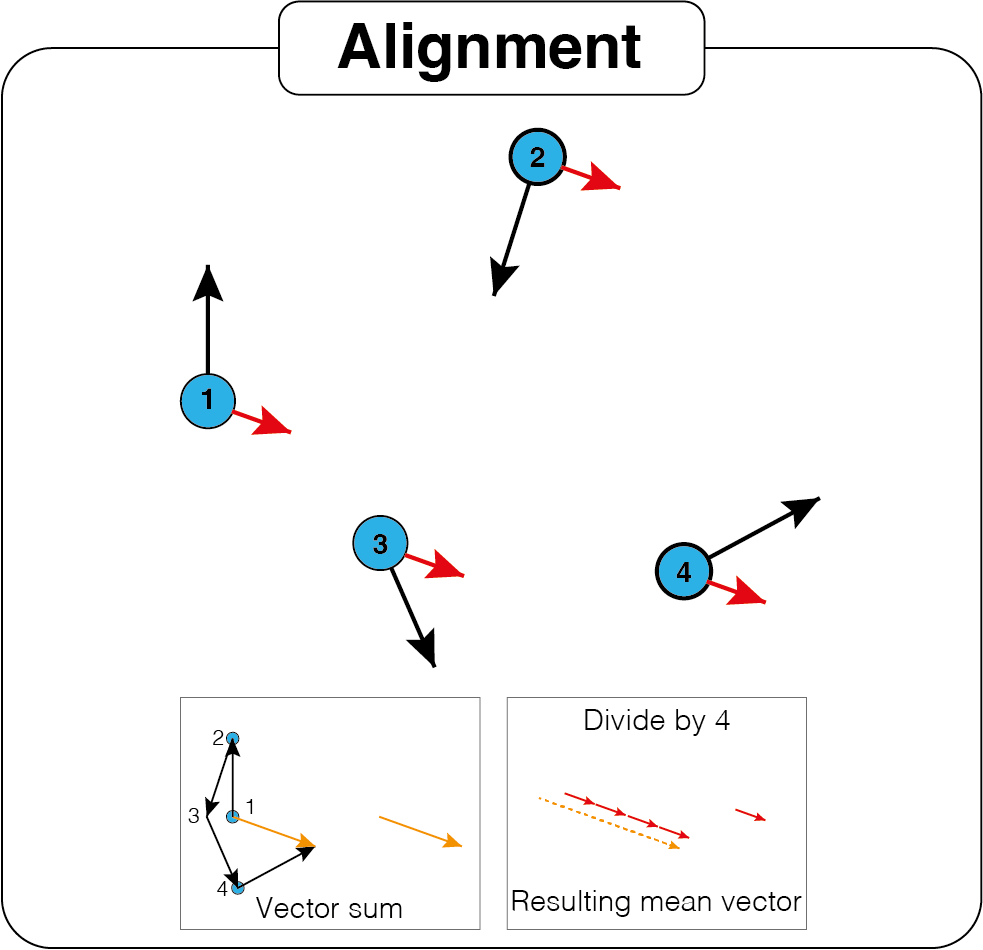
alignment

def matchVelocities(x_prev, y_prev, x0, y0, n, neighbors_dist, match_velocity):
    m = squareform(pdist(np.transpose([x_prev,y_prev])))
    idx = (m<=neighbors_dist) # & (m!=0)
    
    vmean_x = np.zeros(n)
    vmean_y = np.zeros(n)
    for i in range(0, n-1):
        vmean_x[i] = np.mean( x0[idx[i,]] - x_prev[idx[i,]] )
        vmean_y[i] = np.mean( y0[idx[i,]] - y_prev[idx[i,]] )
    
    return vmean_x*match_velocity, vmean_y*match_velocity

Put all together

In this block the velocities from the 3 rules are add together to update the actual velocity. The resulting velocity is then restricted to the maximum velocity (otherwise, it happens that they reach unrealistic velocities and moves like atoms in a very hot gas)

Velocities are also corrected in order to avoid walls. When a boid come closer than margin to a wall, a wall_repulsion applied opposite to the direction of the wall.

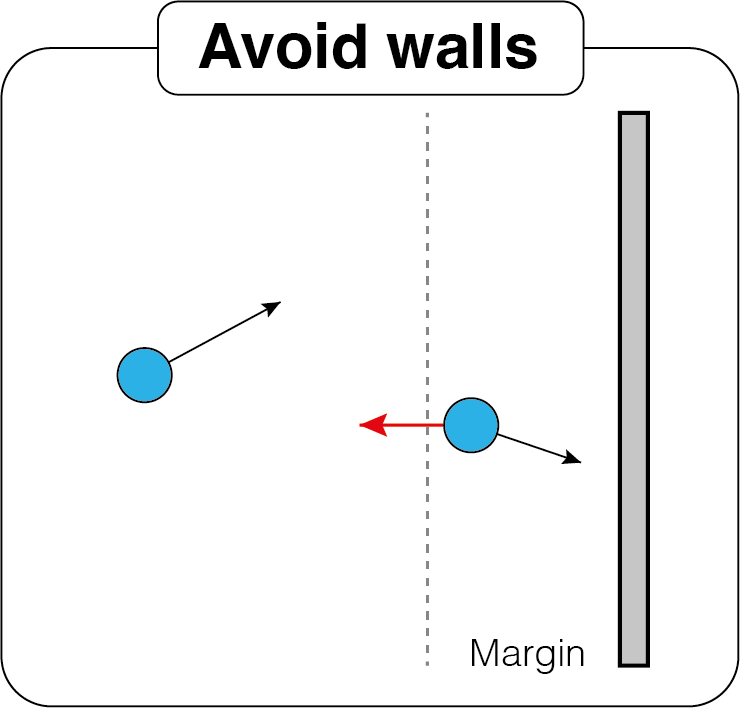
wall_repulsion

def move(x0,y0, x_prev, y_prev, n, neighbors_dist, R, privacy, bird_repulsion, match_velocity, L, margin, wall_repulsion, max_speed):
    
    vx1,vy1 = moveToCenter(x0,y0, neighbors_dist, n, R)
    vx2,vy2 = avoidOthers(x0,y0,  n, privacy, bird_repulsion)
    vx3,vy3 = matchVelocities(x_prev, y_prev, x0,y0,  n, neighbors_dist, match_velocity)

    vx = x0-x_prev + vx1 + vx2 + vx3 
    vy = y0-y_prev + vy1 + vy2 + vy3     
    
    # max speed limit
    # Matrix 2xn. Get the length of the velocity vector for each boid, and 
    # scale it with the maximum value
    v_norm = np.zeros((2,n))
    v_vector = np.array([vx,vy])
    norm = np.linalg.norm(v_vector, axis=0)
    v_norm[:, norm!=0] =  v_vector[:, norm!=0]/norm[norm!=0]*max_speed
    
    vx = v_norm[0,:]
    vy = v_norm[1,:]
    
    # Dump velocity when hits a wall    
    right_border_dist  = L - x0
    left_border_dist   = x0 + L
    upper_border_dist  = L - y0
    bottom_border_dist = y0 + L
    
    vx[right_border_dist < margin] = vx[right_border_dist < margin] - wall_repulsion
    vx[left_border_dist < margin] = vx[left_border_dist < margin] + wall_repulsion
    vy[upper_border_dist < margin] = vy[upper_border_dist < margin] - wall_repulsion
    vy[bottom_border_dist < margin] = vy[bottom_border_dist < margin] + wall_repulsion
    
    x1 = x0 + vx
    y1 = y0 + vy
    
    x1 = np.round(x1)
    y1 = np.round(y1)
    
    return x1,y1

Animate

for t in range(1,tsteps-1):
    x[:, t+1],y[:, t+1] = move(x[:, t],y[:, t], x[:,t-1],y[:,t-1],
                               n, neighbors_dist, R, privacy, bird_repulsion, match_velocity, 
                               L, margin, wall_repulsion, max_speed)
    
def init():
    points.set_data([], [])
    return points,

def animate(i):
    xx = x[:,i]
    yy = y[:,i]
    points.set_data(xx, yy)
    return points,

anim = FuncAnimation(fig, animate, init_func=init,
                                frames=tsteps-2, interval=80, blit=True)

from IPython.display import HTML
HTML(anim.to_html5_video())

Final animation

complete_animation

Here you can see the separate contribution of the 3 rules, the final result is a superposition of these 3 effects.

Only rule 1: cohesionOnly rule 2: separationOnly rule 3: alignment
   

References