Wordle is an online game designed by Josh Wardle (no pun intended). The goal is to guess a 5 letters word, given 3 types of clues derived by the game: right letter in the right place (green), right letter but in the wrong place (yellow) and the letter is not in the target word (grey). There are 2315 possible target word that you can find in this list.

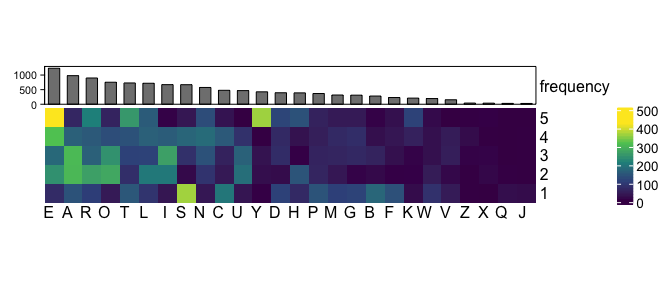
An intuitive strategy could be to start with a word created from the combination of the most common letters. You can see from this heatmap where the rows are the position along the word and the column are the letter that the 6 most common letters are E A R O T L. I initially used to start with the word “LATER”, but this choice turned out to be suboptimal.

There is a finer strategy to win at wordle and it involves information theory concepts.

Strategy intuition

When we try to guess the target word we have \(3^5\) so 243, possible colors configuration, which is less that the dimension of the target dictionary (2315). This means that given a guess, some color configurations will be repeated for different target words.
Let’s take for example the word CIGAR:

• 1 [green]-[green]-[green]-[green]-[green] configuration (when the target is CIGAR itself).
• 3 [green]-[green]-[grey]-[grey]-[grey] configurations (CIVIC, CINCH and CIVIL).
• 360 configurations (!) with [grey]-[grey]-[grey]-[grey]-[grey] (E.g. HELLO / FLUSH / LEMON …).

Therefore if I start with the word CIGAR and get [green]-[green]-[grey]-[grey]-[grey], that would be super surprising (or informative) because I would be left with only 3 other words. But getting an [green]-[green]-[grey]-[grey]-[grey] as response is also highly unlikely, because it happens only with 3 words out of 2315

\[\frac{3}{2315} = 0.001\]

GOAL: We need to find a guess word that on average will give me highly surprising (or informative) color configurations

I.e We look for a word that maximises the reduction of the space of possibilities, We want to shrink that 2315 target words dictionary into a smaller set. Sejal Dua in her arcticle explains it well:  

We want to pick the word that yields the largest remaining information. This means that, regardless of if we get a bunch of green and yellow tiles or all grey tiles, we will ensure that all possible outcomes are similar and that none of them are too bad.

Here is when entropy (or information) definition becomes handy.

Entropy

No one really knows what entropy really is.
— Von Neumann -

 

The unity measure of information is the bit. 1 Bit of information is an observation that cuts the world of possibilities in half. Or in other words, that it has \(p = 0.5\) chance of occurrence. The formula for information of an event with probability \(p\) is:

\[I = -log_2(p)\]

which is equal to 1 when \(p = 0.5\).

Information is just a function of the probability of a random variable, but it is useful when we need to talk about space of possibilities, which in this case is the dictionary. In particular, information has an opposite trend with respect to probability: when an event is unlikely it has a small probability, but high information.

The basic intuition behind information theory is that learning that an unlikely event has occurred is more informative than learning that a likely event has occurred.
— Deep Learning, Ian Goodfellow -

 

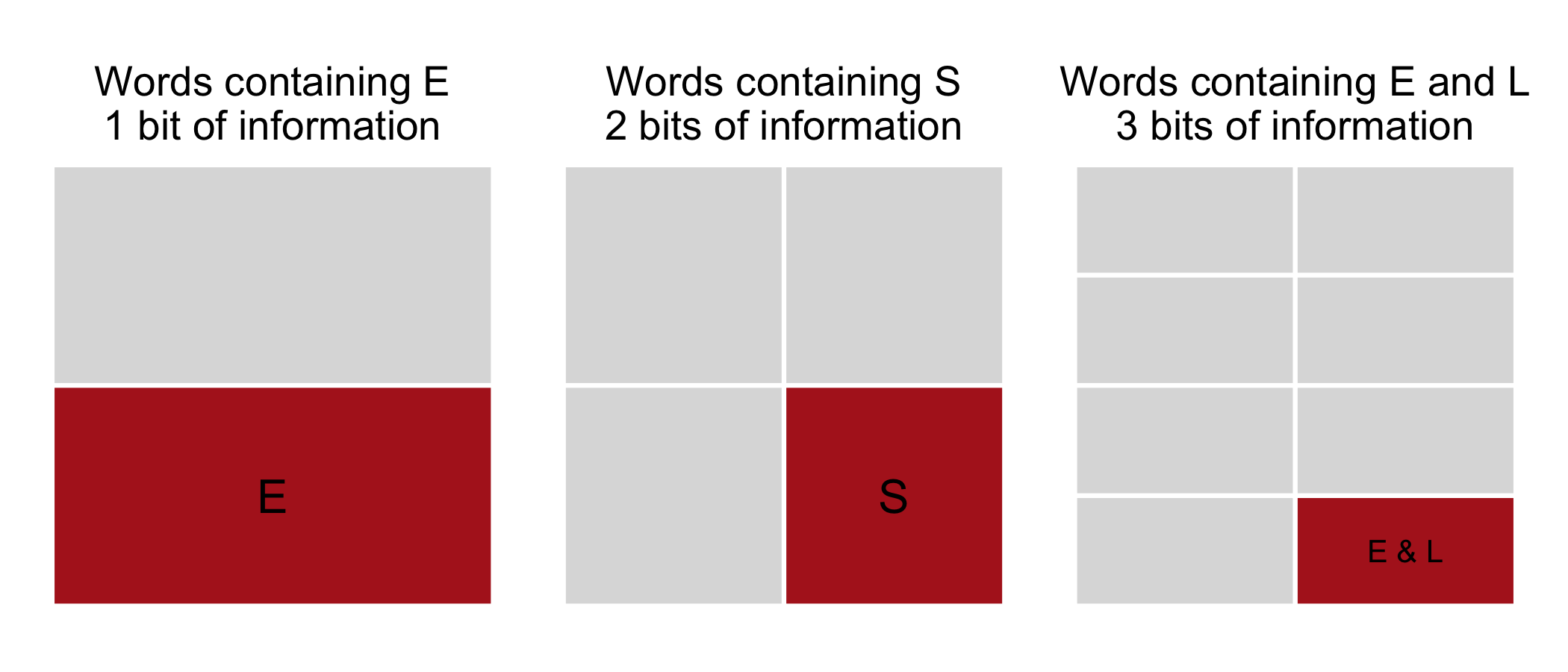
Therefore, unlikely events are also highly informative. For example, words containing the letter E are 1056 out of the 2315, so they account for 45% of the dictionary. So it’s really common to find a word with an E inside, and it would give about 1 (\(-log2(0.45) = 1.15\)) bit of information (not so much then), since it cuts in half the space of possibilities.
Words containing the letter S are rarer (550), in this case this requirement halves the space of possibilities twice (550 / 2315 = 0.24), i.e. it splits it in 4 parts. Words containing both the letters E and L are 280, so in this case this requirement halves the space of possibilities 3 times (280 / 2315 = 0.12), i.e. it splits it in 8 parts.

In the case of wordle we don’t suggest single letter guesses, but combinations of five letters. Therefore we need to consider the information content of the color configurations, rather than single letters.

For each guess we make, we can measure how informative each color configuration is and take the expected value of this information, which is the sum of each color configuration \(c\) information multiplied by its probability of occuring \(p_c\).

\[I[guess] = \sum_{c}p_c \cdot log_2(p_c)\] \[c \in \{ \text{color configurations (total of 243)\}}\]

The resulting value represents the average reduction of the dictionary after choosing the “guess” word. Mathematically it is the expected value of information that the “guess” word gives. It is an average across all the possible 2315 targets, each one of them has one possible color configuation out of the 243 possibility relatively to the “guess” word.

Basically, we loop for each pair of guess and target words, we find the 5 colors associated to it. Then we compute the probability of having a particular color combination, and plug it into the formula.

Best and worst starting words

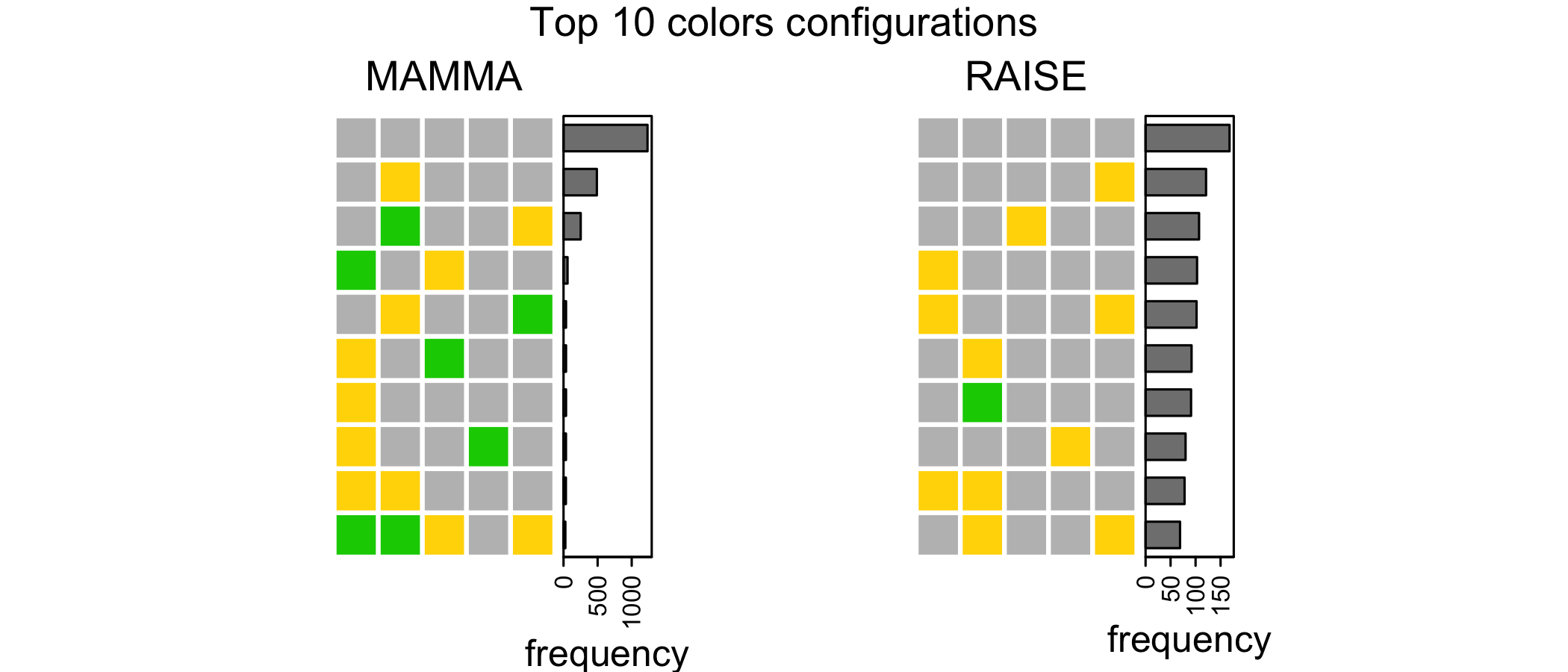
This heatmap shows the frequency of colors distributions for the word with highest expected value of information (the best word, RAISE), and for the word with the lowest (the worst, MAMMA).
The height of the heatmap represents the frequency that each color configuration has, from the most common one at the bottom, to the rarest at the top.

Here you see a clear visualization of the information of the starting word.

The word MAMMA about half of the time would give all greys, which would only split the dictionary in half, not much of a gain. Just in the case that the target word is among the ones at the top of the matrix MAMMA would give an high information gain, but to have that restricted set of words as targets is really unlikely.

The term MAMMA is a low entropy, or low information, opening word.

While RAISE has a more homogeneous pattern of color configurations: whatever the target word is, we are ensured to have an overall good shrink of the dictionary.

RAISE is a high entropy, or high information, opening word.

We can visualize it in a different manner by plotting on x the all possible color configurations and on y their frequencies, or probabilities. Looking at the shape of the two distribution you can see that information is maximized when the probability distribution tends to uniform, in other words when the probabilities of color configurations spread out.
Even if MAMMA is probably the first word we said in real life, it is the worst word to start with in WORDLE. This is because MAMMA has many repeated letters that won’t give any information gain.

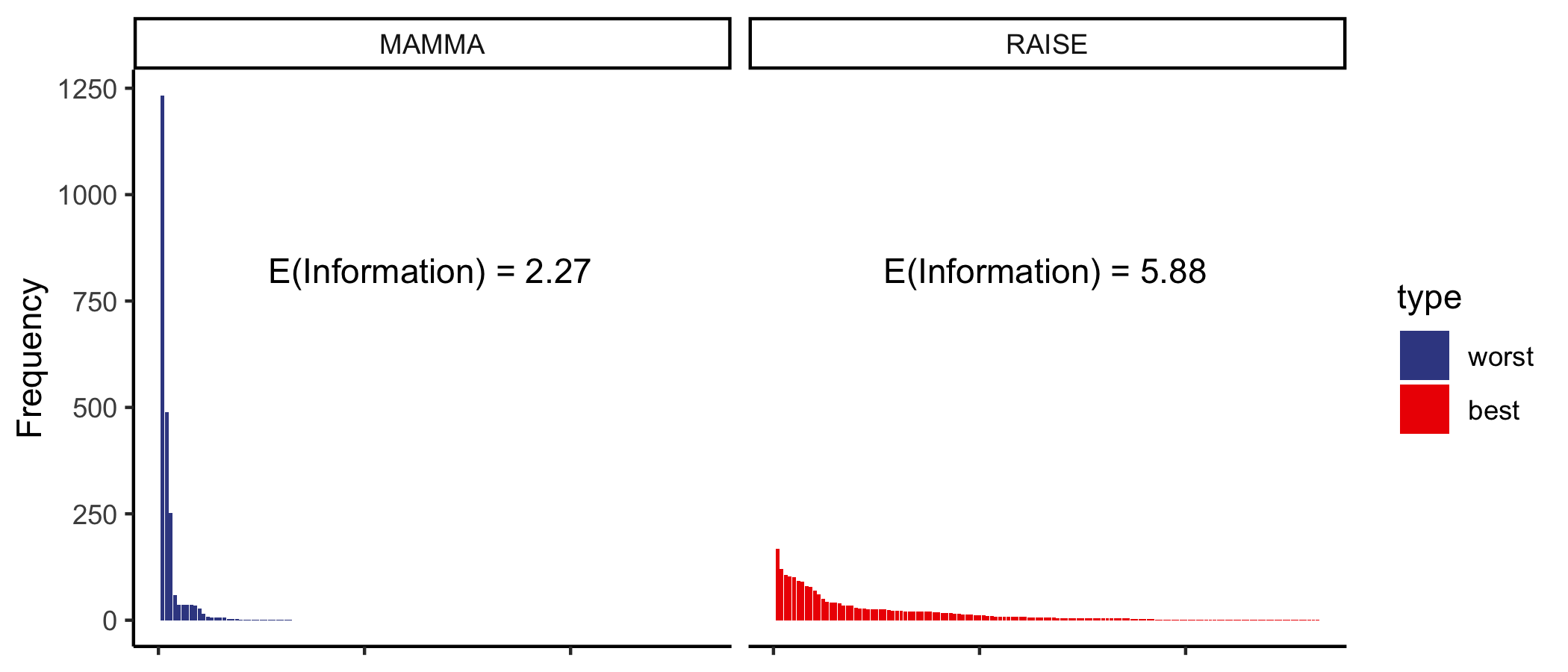
RAISE has an information expected value of 5.88, this means that on average this guess will halve the dictionary almost 6 times, so the average dictionary size reduction will be from 2315 to

\[\frac{2315}{2^{5.88}} \sim 39\]

For MAMMA the reduction would be from 2315 to:

\[\frac{2315}{2^{2.27}} \sim 480\]

Performance

I run a simulation with 500 random target words from the list of 2315 words and using the most and the less informative word RAISE and MAMMA as first guesses.

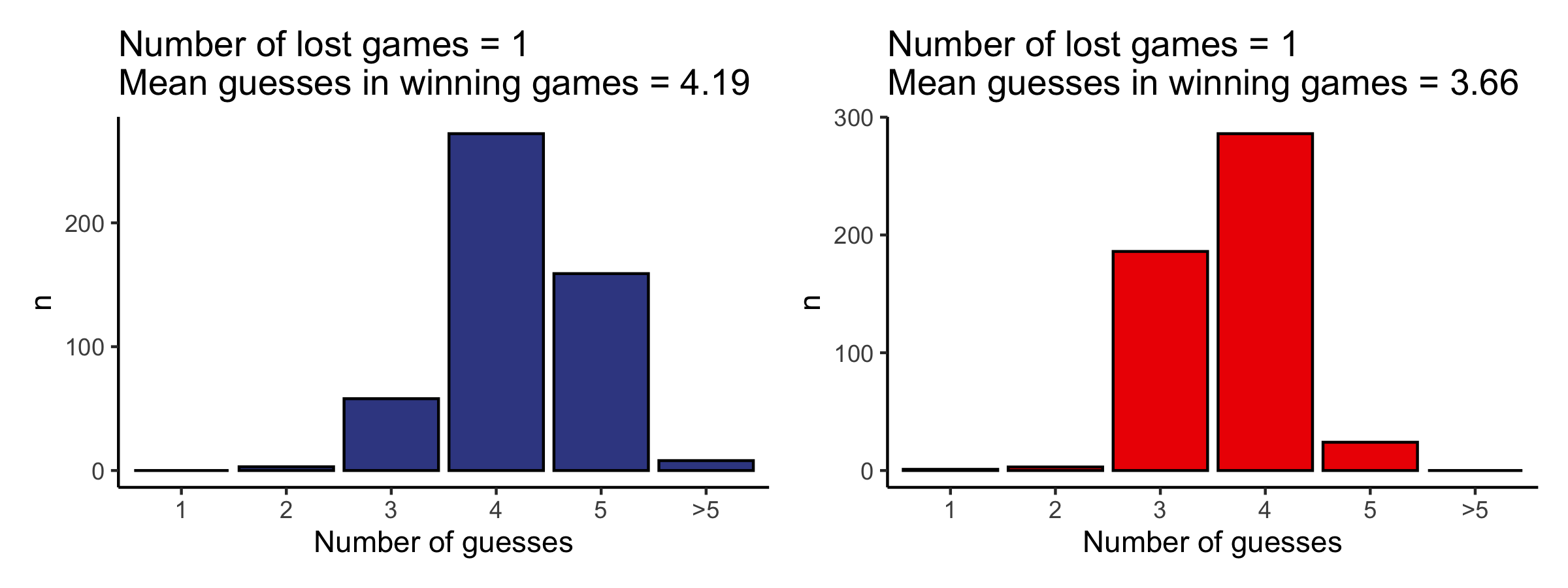
Conclusions

Entropy is a mess. It is always tricky to understand and to explain concepts related to probability distributions. The main message here is that a system that has few possible configurations with heterogeneous probabilites has a low entropy (and low information). In the wordle case this system would be the game starting with the word MAMMA. while the system with many configuration with almost equal probability of occurring is a high entropy (or high information) system. This is the case of the wordle game starting with RAISE.

I like Matthew N. Bernstein’s definition of entropy as degree of uniformness of a random variable:

The higher the entropy of a random variable, the closer that random variable is to having all of its outcomes being equally likely.

Note: For semplicity (and for limited computational resources) in this article I will only used the 2315 target words and not all the possible 5 letters words in the english dictionary as guess words. This is why the worst and best words in this article are different from the Andrew Steele’s video since he used all the 5 letter words in the english dictionary. This can change the probability distributions and consequently the starting words. His best word is SOARE, which is not among the target words list.

“If you guessed a coin flip correctly, how surprised would you be?
A bit.”

Explaination: a fair coin has 2 faces with equal outcome probabilities (0.5). The probability of having a head is 0.5, so you would be \(-log_2( 0.5 ) = 1\) bit surprised of getting it. In other words, each of the two outcomes split the world of possibilities in half, from 2 possibilities to 1 possibility.

References

• This analysis is strongly inspired by 3Blue1Brown video, corrected in this new video
• Ask a mathematician, ask a physicist - What’s the relationship between entropy in the information-theory sense and the thermodynamics sense? arcticle
• Claude Shannon - “A Mathematical Theory of Communication” paper
• Sejal Dua’s “A Deep Dive into Wordle, the New Pandemic Puzzle Craze” arcticle
• Another related video: Andrew Steele’s video
• Matthew N. Bernstein’s definition of entropy as measure of uniformness
• Plots are generated in R enviroment using ggplot2 and ComplexHeatmap